Starting with this post, I want to venture into a new area — investing — distinct from my usual topics of computer vision, deep learning, etc. Investing has become my latest hobby, and after diving into it, I have found it both fascinating and inspiring.
In this first post, I will explore a fundamental concept in the world of investing: compound interest. To me, it represents the “first principle” of investing.
What is Compound Interest?
Compound interest is a form of interest. When you deposit money into a bank account or lend it to someone, you typically earn interest. The amount you deposit or lend is called the principal, and the interest is calculated as a percentage (interest rate) of the principal. For example, if you have a principal of $100 and an interest rate of 10%, your interest would be $10 ($100 x 10% = $10).
Interest is typically paid at fixed intervals. In the example above, let’s assume the $10 is paid annually. After the first year, you would have $100 in principal and $10 in interest. Now, imagine that the $10 interest is added to the $100 principal. This means that, in the next period, interest will be calculated based on the new principal amount of $110. If the interest rate remains at 10%, your next interest payment will be $11 ($110 x 10% = $11).
Here, you may notice a snowball effect: as your interest payments are added to your principal (increasing it from $100 to $110), your interest payments also grow (from $10 to $11). This cycle continues, with the interest added to your principal, which increases the principal further, leading to higher interest payments and, in turn, an even higher principal, and so on.
If we continue the above calculations for 10 years, the principals and interest amounts would look as follows (with rounding errors). The principal represents the total amount (principal plus interest) at the beginning of each year, which is the same as the total at the end of the previous year. The interest is the amount earned at the end of each year. For year n + 1, the principal is simply the principal from year n plus the interest earned in year n.
| Year | Principal ($) | Interest ($) | Total ($) |
|---|---|---|---|
| 1 | 100 | 10 | 110 |
| 2 | 110 | 11 | 121 |
| 3 | 121 | 12.1 | 133.1 |
| 4 | 133.1 | 13.31 | 146.41 |
| 5 | 146.41 | 14.641 | 161.051 |
| 6 | 161.051 | 16.1051 | 177.1561 |
| 7 | 177.1561 | 17.7156 | 194.8717 |
| 8 | 194.8717 | 19.4872 | 214.3589 |
| 9 | 214.3589 | 21.4359 | 235.7948 |
| 10 | 235.7948 | 23.5795 | 259.3742 |
The magic of Compound Interest
“Compound interest is the eighth wonder of the world. He who understands it, earns it… he who doesn’t… pays it.” - Albert Einstein
Looking at the numbers in the table above, you might realize the magic of compound interest: starting with $100 in principal, earning 10% interests per year, by the beginning of the 9th year, you have doubled your money. If this doesn’t amaze you, let’s explore two more calculations to help you fully appreciate it.
Compounding for Another 10 Years
Let’s extend the calculations from the table above for another 10 years.
| Year | Principal ($) | Interest ($) | Total ($) |
|---|---|---|---|
| 11 | 259.3742 | 25.9374 | 285.3117 |
| 12 | 285.3117 | 28.5312 | 313.8428 |
| 13 | 313.8428 | 31.3843 | 345.2271 |
| 14 | 345.2271 | 34.5227 | 379.7498 |
| 15 | 379.7498 | 37.9750 | 417.7248 |
| 16 | 417.7248 | 41.7725 | 459.4973 |
| 17 | 459.4973 | 45.9497 | 505.4470 |
| 18 | 505.4470 | 50.5447 | 555.9917 |
| 19 | 555.9917 | 55.5992 | 611.5909 |
| 20 | 611.5909 | 61.1591 | 672.7500 |
As you can see, at the beginning of the 10th year, your principal is around $236. By the start of the 20th year, it has grown (non-linearly) to approximately $612. Continuing the calculations, by the 26th year, you will receive an interest payment of $108.35, the first time your interest payment exceeds your initial $100 principal! The longer you continue the calculations, the wilder the numbers become.
The Case of Non-Compounding
Now, let’s consider the non-compounding case, where the annual interest payment is not added back to the principal. In this scenario, you receive interest based on the initial $100 principal, meaning you earn $10 in interest each year. After 10 years, your total amount would be $200 ($100 + $100 x 0.1 x 10). While this is not too far from the compounded case, where your total would be around $259, the gap widens significantly after another 10 years. In the non-compounding case, you would have $300 ($100 + $100 x 0.1 x 20), while in the compounding case, you would have approximately $673. As before, the longer you continue the calculations, the more drastic the gap becomes.
Exponential Explosion
The snowball effect of compound interest described above is known as exponential growth, or more dramatically, exponential explosion. This is the essence of the magic of compound interest — over time, the amount of your money grows exponentially to a “formidable” sum (though not so dramatic in the example above, largely due to the small $100 principal).
If we plot the results of compounding versus non-compounding over 50 years, the “explosion” or magic of compound interest becomes much more evident. After 50 years, your initial $100 principal grows to around $11,739! And remember, this 117-fold growth comes from a “modest” 10% compound interest rate. Take a moment to think about it: a 117-times increase from just 0.1, and you will start to appreciate the magic of compound interest. By comparison, in the non-compounding case, it would take 1,164 years to grow to $11,739!
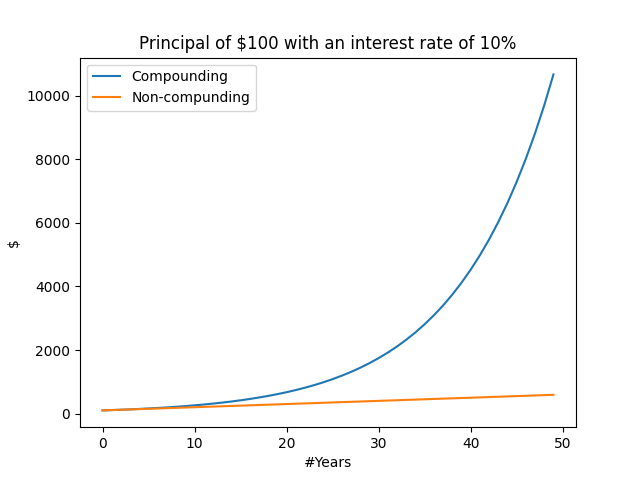
For what it’s worth, the non-compounding case is also known as simple interest.
Why Care About Compound Interest
Now that we understand compound interest, why is it important to investing? The answer is simple: it measures your return on investment. If you are familiar with investing, you have likely heard terms like “the annualized rate of return is X% over the past Y years”. This “annualized rate of return” is similar (but not identical) to the compound interest rate we discussed earlier. As we have seen, compound interest has the magic to grow your money into a formidable sum over time.
Misconceptions
While the “annualized rate of return” is similar to the compound interest rate in our example, there is a crucial difference that often leads to misconceptions. In our compound interest example, the 10% interest rate is fixed every year. However, in real-world investing, the rate is almost never fixed. For instance, an annualized rate of return of 10% does NOT mean you are guaranteed to earn 10% each year! Instead, the annualized rate of return is calculated by comparing the starting and ending values of an investment over a given time period and determining the equivalent compound interest rate. If you are interested in how it is computated, you can play with it using this calculator.
It is crucial for all investors to dispel this misconception and set realistic expectations.
Why Compounding Is a Double-Edged Sword
From the discussions above, I hope you now appreciate the magic of compounding in investing. However, it is equally important to understand why compounding can become a double-edged sword. The reason is simple: while compounding can work wonders, it can also work against you.
In the real world, investing is not free. While the market might generate an annualized return of 10%, you don’t get to keep all of it. A portion is deducted as investment costs. A common example of such costs is the total expense ratio (TER) of investment funds, where you pay a percentage of your money to the fund providers each year. When it comes to costs, compounding works against you.
Let’s revisit the compound interest example of 10% and consider a principal of $10,000. Suppose the TER is 1%. After one year, your gross amount would grow to $11,000 ($10,000 x 10%). However, you would pay $100 ($10,000 x 1%) in fees to the fund providers, leaving you with a net amount of $10,900. Effectively, your net compound interest rate is 9%. This leads to the following simple and clean formula:
Net annualized rate of return = Gross annualized rate of return - Total expense ratio
or
Investment return rate = Market return rate - Total expense ratio
Now, let’s perform similar calculations to compare a 10% market return with a 9% investment return. Specifically, we will calculate the total amount of money (with rounding errors) at 10-year intervals for both cases.
| Years | Market Value (10%, $) | Investment Value (9%, $) | Percentage of Market Value Kept by Investment (%) |
|---|---|---|---|
| 10 | 25,937.42 | 23,673.64 | 91.27 |
| 20 | 67,275.00 | 56,044.11 | 83.31 |
| 30 | 174,494.02 | 132,676.78 | 76.04 |
| 40 | 452,592.56 | 314,094.20 | 69.40 |
| 50 | 1,173,908.53 | 743,575.20 | 63.34 |
From the table, it is clear that over time, you retain less and less of the market value. After 10 years, you keep over 91%, but after 50 years, this drops to just over 63%. In other words, after 10 years, you lose around 9% of the market value, and after 50 years, the loss grows to 37%. Where does this 37% go? You guessed it - it’s consumed by fees.
Now, consider this: the 37% loss stems from a seemingly “small” 1% annual fee. To better understand the impact, let’s look at the absolute dollar amounts lost due to these fees over time.
| Years | Market Value (10%, $) | Investment Value (9%, $) | Value Lost to Fees ($) |
|---|---|---|---|
| 10 | 25,937.42 | 23,673.64 | 2,263.79 |
| 20 | 67,275.00 | 56,044.11 | 11,230.89 |
| 30 | 174,494.02 | 132,676.78 | 41,817.24 |
| 40 | 452,592.56 | 314,094.20 | 138,498.36 |
| 50 | 1,173,908.53 | 743,575.20 | 430,333.32 |
As shown, over 50 years, you lose a staggering $430,333 to fees — more than 43 times your initial $10,000 principal! Once again, this immense loss results from a seemingly “small” 1% annual fee.
By now, it should be clear: costs also compound, and over time, they can amount to a formidable loss. This is why compounding can be a double-edged sword.
Caveat 1: Losses Are Not Equal to Fees
It is important to clarify that while the loss is caused by fees, the loss itself is not equal to the fees you pay. In the above example, although you lose $430,333 over 50 years, this doesn’t mean the fund providers receive fees totaling this amount. They actually collect a much smaller sum, around $81,508. This difference arises because the fees you pay stop compounding along with the rest of your investment. If those fees were not deducted, they would have compounded as well, resulting in a significantly higher total value.
Caveat 2: Variable Actual Returns
It is important to note that, for simplicity, we use the annualized rate of return similar to a fixed compound interest rate to illustrate how costs impact returns. However, the math demonstrating the effect of costs remains valid even when applied to variable actual returns.
Let’s consider a simple example where the market drops by 10% in the first year and grows by 20% in the second year. This results in an annualized rate of return of approximately 3.92% over two years (you can verify it using this calculator). Assuming a TER of 1%, we will calculate the end value using both the variable actual returns and the annualized rate of return in the following tables.
Using Variable Actual Returns
| Year | Market Value ($) | Investment Value ($) |
|---|---|---|
| 1 | 900 | 890 |
| 2 | 1,068 | 1,059.1 |
- In the first year, the market value drops by 10% ($1000 x (1 - 10%) = $900). And deducting a 1% fee ($1000 x 1% = $10), the investment value is $890 ($900 - $10).
- In the second year, the market grows by 20% ($890 x (1 + 20%) = $1,068). And deducting a 1% fee on the initial investment value ($890 x 1% = $8.9) , the final investment value is $1,059.1 ($1,068 - $8.9).
Using Annualized Rate of Return
| Year | Market Value ($) | Investment Value ($) |
|---|---|---|
| 1 | 1039.2 | 1029.2 |
| 2 | 1069.54 | 1059.25 |
- Here, we apply the annualized rate of return (3.92%), reduced by the TER of 1%, resulting in a net return of 2.92%. The calculations follow the same logic as the fixed compound interest example.
As shown in the tables above, the final values are very similar (up to rounding differences), regardless of whether we use the variable actual returns and the fixed annualized rate of return. This demonstrates that using the annualized rate still accurately reflects the impact of costs while simplifying the calculations.
Caveat 3: Costs Based on Final Value
In our examples, costs are calculated based on the initial value at the beginning of each year, which allows for the clean formulas presented above. However, if costs are instead calculated based on the final value at the end of each year, the results will differ, though the impact of costs would still be similar.
Let’s revisit the example with fixed 10% annual rate of return and an initial principal of $10,000. This time, a 1% cost is deducted at the end of the year. The numbers would look as follows.
| Years | Market Value ($) | Investment Value ($) |
|---|---|---|
| 10 | 23,694.28 | 23,457.34 |
| 20 | 55,580.49 | 55,024.69 |
| 30 | 130,377.06 | 129,073.29 |
| 40 | 305,829.94 | 302,771.64 |
| 50 | 717,395.74 | 710,221.78 |
In this scenario, the net rate of return drops to approximately 8.9% (you can verify it using this calculator), which is slightly lower than (but similar to) the 9% achieved when costs are calculated based on the initial value.
How to Avoid the Double-Edged Sword
The solution is simple: minimize investment costs, or at the very least, reduce them to a level you can accept. For instance, if the fund cost is reduced to a TER of 0.03% (and such low-cost funds do exist), you would still be able to retain over 98% of the market value after 50 years!
| Years | Market Value (10%, $) | Investment Value (9.97%, $) | Percentage of Market Value Kept by Investment (%) |
|---|---|---|---|
| 10 | 25,937.42 | 25,866.77 | 99.73 |
| 20 | 67,275.00 | 66,908.99 | 99.46 |
| 30 | 174,494.02 | 173,071.98 | 99.19 |
| 40 | 452,592.56 | 447,681.35 | 98.91 |
| 50 | 1,173,908.53 | 1,158,007.18 | 98.65 |
Is My Fund Cost High?
I have seen people ask this question when evaluating whether to select a fund: “Is this X% fund cost high?” To answer this question, you can simply repeat the calculations I provided earlier. Determine the percentage of money that you would lose to fees over your investment horizon and decide whether that percentage is acceptable to you. If you find it unacceptable, the fund cost might be considered high, and you may want to consider looking for one with lower fees.
Summary
John C. Bogle aptly summarized the concepts discussed in this post as “The magic of compounding investment returns” and “The tyranny of compounding investment costs” in his book, The Little Book of Common Sense Investing. This post is heavily inspired by Mr. Bogle’s insights.
Disclaimers
I am not a professional investor or financial advisor, nor do I claim to be. You are solely responsible for your financial decisions. I do not accept responsibility for any inaccuracies in this blog post. The content reflects my personal research and understanding and should not be interpreted as professional advice.